Particle Swarm Optimization Homework

Particle Swarm Module Homework

    For the six hump camelback function (from the earlier homework) below do the following:

   1. Code a simple full model PSO with to solve the problem.  To do this you need to encode the problem as two real variables with associated p and v vectors, and select values for Ѱ₁ and Ѱ₂

   2. Run your PSO for ten different seeds.

   3.  Vary the number of particles and Ѱ₁ and Ѱ₂ values with the PSO from just above (full model).

   4. Draw the convergence graph with different particles number and past it your homework

   5. Please include your code with your homework and summarize your results.

    

1.     FONKSİYON İÇİN ÇÖZÜMLER

MATLAB SCRİPT KODU:

function z = Pfunction(x,y)

    z = (4 - 2.1*x.^2 + x.^4/3).*x.^2 + x.*y +(-4+4*y.^2).*y.^2;

end

oldGLZ=100;

for t=1:1

globalbestX = 0;

globalbestY = 0;

n=20; m=1000;

C1 = 0.5; C2 = 0.5;

fprintf('\n C1=%d, C2=%d, İterasyon=%d \n',C1,C2,m);

    seed=t;

    for i=1:n               

    %X(i) = rand()*5; Y(i) = rand()*5; Vx(i) = rand()*5; Vy(i) = rand()*5;

    X(i) = rand()*((rand()>0.5)*2-1)*3;

    Y(i) = rand()*((rand()>0.5)*2-1)*2;

    Vx(i) = 0;

    Vy(i) = 0;

    pbestX(i) = X(i);

    pbestY(i) = Y(i);

        if (Pfunction(pbestX(i), pbestY(i))) < (Pfunction(globalbestX, globalbestY))      

            globalbestX = X(i); globalbestY = Y(i);

        end

    end           

           

    for iteration=1:m

        for i=1:n

            if (Pfunction(pbestX(i), pbestY(i)) > Pfunction(X(i), Y(i)))       

                pbestX(i) = X(i); pbestY(i) = Y(i);

            end

            if Pfunction(pbestX(i), pbestY(i)) < Pfunction(globalbestX, globalbestY)            

                globalbestX = X(i); globalbestY = Y(i);

            end

        end      

        for i=1:n                   

            Vx(i) = Vx(i) + C1 * rand() * (pbestX(i) - X(i)) + C2 * rand() * (globalbestX - X(i));

            Vy(i) = Vy(i) + C1 * rand() * (pbestY(i) - Y(i)) + C2 * rand() * (globalbestY - Y(i));

            X(i) = X(i) + Vx(i); Y(i) = Y(i) + Vy(i);

            if X(i)<-3 || X(i)>3

            X(i) = rand()*((rand()>0.5)*2-1)*3;

            end       

            if Y(i)<-2 || Y(i)>2

            Y(i) = rand()*((rand()>0.5)*2-1)*2;

            end

        end

       

        GLX(iteration) = globalbestX;

        GLY(iteration) = globalbestY;

        GLZ(iteration) = Pfunction(globalbestX,globalbestY);

        if GLZ(iteration)<oldGLZ

        Gereken_it=iteration;

        oldGLZ=GLZ;

        end

       

    end

            GX = globalbestX; GY = globalbestY;

            GZ = Pfunction(GX,GY);

            fprintf('Seed %d, GZ = %f, GlobalX = %f, GlobalY = %f \n',seed,GZ,GX,GY);

end

% Fonksiyon Çizimi

dx = 0.03; %Çizim Sıklığı

Xlimits = -2:dx:2; % Çizim X ekseni sınırları

Ylimits = -1.5:dx:1.5; % Çizim Y ekseni sınırları

[X,Y] = meshgrid(Xlimits,Ylimits);

Z = Pfunction(X,Y);

subplot(211); surf(Y,X,-Z);

grid on;

xlabel('x');

ylabel('y');

zlabel('z');

hold on

%bulunan f değerinin çizilen grafik üzerince işaretlenmesi.

subplot(211); plot3(GY,GX,-GZ, 'b*');

it=1:1000;

subplot(212); plot(it,GLZ),xlabel('iterasyon sayısı'), ylabel('Global_Z')

hold on;

plot(Gereken_it,GLZ(Gereken_it),'b*')

grid on;

PROGRAMIN KOŞTURULMASI:

Örnek:1

Yakınsama Grafiği:

Örnek:2

Yakınsama Grafiği:

10 Farklı Seed Değeri İçin Sonuçlar:

2.     FONKSİYON İÇİN ÇÖZÜMLER

MATLAB SCRİPT KODU:

function z = Pfunction2(x,y)

z=-( (sin(x) .* (sin((1 * x.^2)/pi)).^20) + (sin(y) .* (sin((2 * y.^2)/pi)).^20) );

end

oldGLZ=100;

for t=1:10

globalbestX = 0;

globalbestY = 0;

n=40; m=1000;

C1 = 1.1; C2 = 1.1;

fprintf('\n C1=%d, C2=%d, İterasyon=%d \n',C1,C2,m);

    seed=t;

    for i=1:n               

    X(i) = rand()*pi; Y(i) = rand()*pi;

    %X(i) = rand()*((rand()>0.5)*2-1)*3;

    %Y(i) = rand()*((rand()>0.5)*2-1)*2;

    Vx(i) = 0;

    Vy(i) = 0;

    pbestX(i) = X(i);

    pbestY(i) = Y(i);

        if (Pfunction2(pbestX(i), pbestY(i))) < (Pfunction2(globalbestX, globalbestY))      

            globalbestX = X(i); globalbestY = Y(i);

        end

    end           

           

    for iteration=1:m

        for i=1:n

            if (Pfunction2(pbestX(i), pbestY(i)) > Pfunction2(X(i), Y(i)))       

                pbestX(i) = X(i); pbestY(i) = Y(i);

            end

            if Pfunction2(pbestX(i), pbestY(i)) < Pfunction2(globalbestX, globalbestY)            

                globalbestX = X(i); globalbestY = Y(i);

            end

        end      

        for i=1:n                   

            Vx(i) = Vx(i) + C1 * rand() * (pbestX(i) - X(i)) + C2 * rand() * (globalbestX - X(i));

            Vy(i) = Vy(i) + C1 * rand() * (pbestY(i) - Y(i)) + C2 * rand() * (globalbestY - Y(i));

            X(i) = X(i) + Vx(i); Y(i) = Y(i) + Vy(i);

            if X(i)<0 || X(i)>pi

            X(i)= rand()*pi;

            end       

            if Y(i)<0 || Y(i)>pi

            Y(i)= rand()*pi;

            end           

        end     

    

        GLX(iteration) = globalbestX;

        GLY(iteration) = globalbestY;

        GLZ(iteration) = Pfunction2(globalbestX,globalbestY);

        if GLZ(iteration)<oldGLZ

        Gereken_it=iteration;

        oldGLZ=GLZ;

        end

       

    end

            GX = globalbestX; GY = globalbestY;

            GZ = Pfunction2(GX,GY);

            fprintf('Seed %d, GZ = %f, GlobalX = %f, GlobalY = %f \n',seed,GZ,GX,GY);

end

%fonksiyonun çizdirilmesi

[x,y]=meshgrid(0:.03:pi,0:.03:pi);

z=Pfunction2(x,y);

subplot(211); surf(x,y,z);

hold on

%bulunan f değerinin çizilen grafik üzerince işaretlenmesi.

subplot(211); plot3(GX,GY,GZ, 'b*');

it=1:1000;

subplot(212); plot(it,GLZ),xlabel('iterasyon sayısı'), ylabel('Global_Z')

hold on;

plot(Gereken_it,GLZ(Gereken_it),'b*')

grid on;

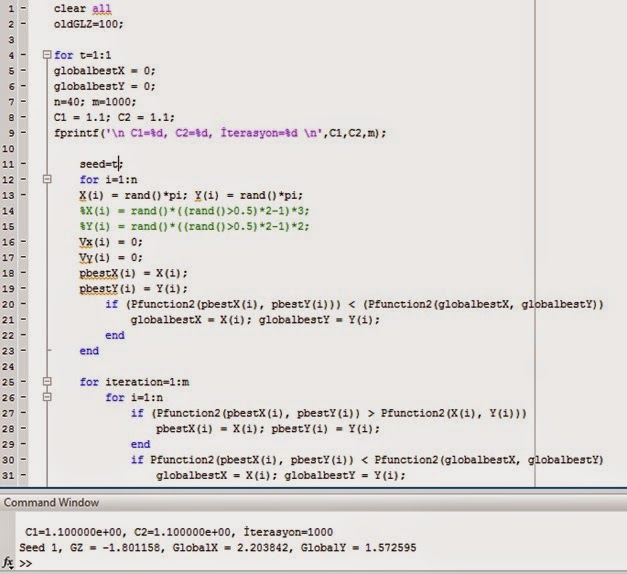
PROGRAMIN KOŞTURULMASI:

Örnek:1

Yakınsama Grafiği:

Örnek:2

Yakınsama Grafiği:

10 Farklı Seed Değeri İçin Sonuçlar:

Kez Görüntülendi.(Views)